Home

Aide - Divers

YachtLINES Autonome

ShipLINES Autonome

Sections

Courbes et Surfaces

Génération Paramétrique de Coque

IntelliHull

X-Topologie, Surfaces Multi-Patch

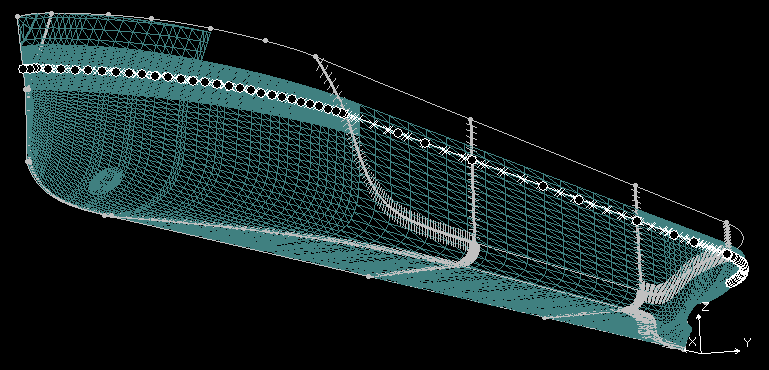
Réutilisation et Reconstruction de la Géométrie de Surface                            Original

Anciennes Géométrie et Formats de Fichiers

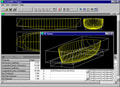
La vaste gamme d'outils de CAO et de formats de fichiers d'échange nous fournit différentes capacités nous permettant d'échanger notre conception entre les systèmes pour obtenir la meilleure capacité au bon moment. Il existe un grand nombre d'outils logiciels et de formats de fichiers de géométrie dans l'industrie maritime. Nous aimons utiliser de vieilles données souvent parce que les caractéristiques de performance de la coque représentée sont connues et parfois c'est la seule représentation qui existe, électroniquement ou autrement. La géométrie de la surface de la coque peut être saisie sous la forme d'Offsets, de surfaces, de facettes occasionnellement ou de maillages linéaires. Il existe également un grand nombre de formats de fichiers propriétaires. Ces données peuvent être archivées et doivent être réutilisées des années plus tard. Comme une grande partie des données est stockée sous forme de texte dans des structures de données communes, il est possible d'extraire des représentations significatives de ces fichiers longtemps après que le logiciel de création a été installé. 

Défis en matière de Modélisation Solide

Aujourd'hui, la modélisation solide est omniprésente, mais les structures de données à l'appui sont complexes et la technique repose sur de nombreuses analyses numériques sensibles aux tolérances. Avec différents outils de modélisation des solides utilisant différents algorithmes, représentations mathématiques et tolérances, il peut y avoir des problèmes occasionnels de chargement de modèles d'un système à l'autre. Si un modèle est passé entre plusieurs systèmes différents, des problèmes peuvent s'accumuler, ce qui entraîne une géométrie corrompue et un modèle défaillant. Pire encore, certains systèmes de modélisation des solides remplacent la géométrie concise, comme les primitives mathématiques ou les plans par une géométrie générique comme les surfaces NURBS. L'utilisateur peut ne pas s'en rendre compte jusqu'à ce que le modèle géométrique échoue et qu'il n'est plus possible de continuer avec cette version de la définition.

Les modèles solides peuvent échouer s'il y a de mauvaises tolérances entre les patches ou des erreurs dans la surface.

Relation Etroite entre la Conception de la Forme de la Coque et la Géométrie de Surface

La conception de la surface de la coque est une discipline unique. Nous sommes l'un des rares champs de conception qui aiment interagir directement avec les polygones de contrôle NURBS ou, pour des formes de coque de navire plus complexes, nous pouvons utiliser des courbes de définition qui forment les composantes de bord de la structure de données B-Rep qui maintient plusieurs patches de surface ensemble comme une'Surface' de modélisation solide à part entière. Les concepteurs marins ont toujours eu une relation étroite avec les représentations mathématiques brutes et les structures de données. C'est bien quand ça marche bien, mais quand les représentations sont utilisées incorrectement, les définitions de surface peuvent échouer et des écarts entre les correctifs apparaîtront. Plus souvent qu'autrement, c'est dû à un manque d'expérience, de compétences ou à l'incapacité de poser les bonnes questions sur les meilleures pratiques ou les capacités des outils. A cela s'ajoute le désir que le logiciel cache son fonctionnement et ses mécanismes internes afin que les utilisateurs peu qualifiés ou expérimentés puissent obtenir des résultats adéquats.

​Sauvetage d'une Géométrie Brisée

Numériser des plans 2D peut être une tâche laborieuse. Nous pouvons utiliser un kutch d'ingénieur et taper les coordonnées dans le logiciel. L'espace sera nécessaire pour mettre en page le papier et nous passerons beaucoup de temps à reconfigurer la position de notre corps pour mesurer, mesurer à nouveau pour vérifier, puis écrire ou taper dans l'ordinateur et ensuite retourner travailler là où nous étions auparavant sur le plan. Un numériseur électronique peut réduire le temps en capturant les coordonnées et en les introduisant dans le logiciel. S'il existe déjà une définition électronique, nous pouvons numériser à l'intérieur de l'environnement de conception en utilisant les caractéristiques d'accrochage de coordonnées dynamiques qui sont présentes dans de nombreuses applications de conception CAO. L'accrochage dynamique vous permet de dessiner interactivement de nouvelles entités géométriques en faisant référence à la géométrie existante et en extrayant les positions des coordonnées des éléments en fonction de la position de la souris. Cela peut être un processus très rapide et c'est quelque chose qui serait considéré comme une opération de routine aujourd'hui.

La façon la plus simple de capturer la géométrie est d'utiliser des outils d'accrochage pour identifier les points. Plus facile, mais qui prend encore du temps et la géométrie tracée nécessite toujours de l'interprétation.

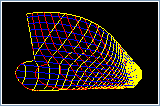
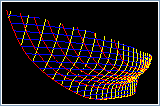
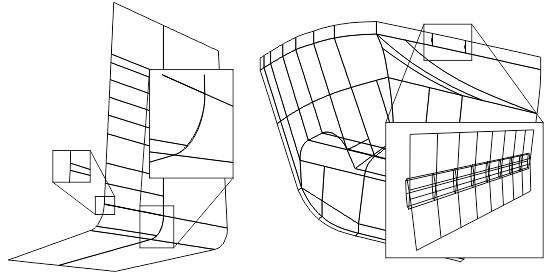
Puisque les logiciel de design de coque utilise souvent une représentation spécialisée, il est très avantageux que des représentations génériques puissent également être importées dans le logiciel et utilisées comme références pour construire une définition de surface de coque à l'aide d'outils d'accrochage. Bien que les outils d'accrochage dynamique se retrouvent dans de nombreux outils de CAO génériques, ce n'est pas quelque chose qui est présent dans tous les outils de conception de surface. PolyCAD a été le pionnier de la capacité d'importer la géométrie primitive et de l'embarquer pour permettre à la définition de la surface de la coque d'être reconstruite et réutilisée. En fait, le snapping a été le développement le plus productif de l'histoire de l'outil. Des exemples de construction des courbes de limites et de caractéristiques d'un réseau de courbes X-Topologie peuvent être trouvés ici pour un ensemble de sections importées et pour une définition de surface existante. (WIP)

Intersection comme Moyen de Numérisation des Coordonnées.

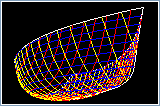
Bien que l'accroche Dynamique soit bon pour capturer des coordonnées à partir de caractéristiques particulières de la géométrie de référence, il n'est pas le seul pour capturer la forme. La capture de forme nécessite une approche plus systématique et forcer l'utilisateur à être systématique dans son utilisation du logiciel engendre souvent un sentiment d'ennui. Dans la conception de la coque, la forme est souvent capturée avec des coupes transversales - des coupes planes à travers la géométrie représentée sous forme de courbe. Par conséquent, pour capturer la forme à partir de n'importe quelle géométrie de référence, nous pouvons la découper avec un plan pour révéler un ensemble de points de coordonnées. Une courbe (polyligne) peut être générée en reliant les points entre eux à l'aide de divers algorithmes de séquençage ou de tri. Les coordonnées des points d'intersection peuvent également être publiées dans l'environnement CAO sous forme de caractéristiques auxquelles les outils d'accroche Dynamique sont sensibles.

Les sections croisées avec un plan identifient les points qui sont reliés en une courbe.

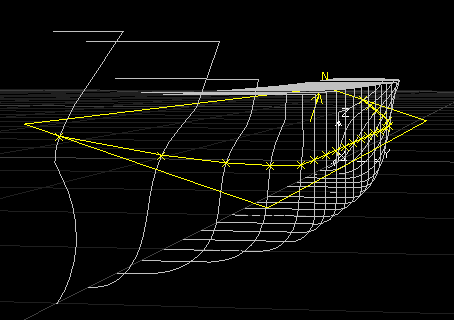
PolyCAD dispose d'un élément Plan qui peut être plus et redéfini de manière interactive. Les options permettent de générer des points basés sur des intersections avec n'importe quelle courbe ou surface. Les courbes peuvent ensuite être générées à travers les points.

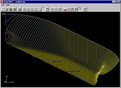
Reconstitution des Surfaces à l'aide de la X-Topologie

Utiliser des plans comme outil pour croiser des points de génération de géométrie qui sont ensuite rassemblés dans une courbe est un moyen efficace de générer une définition de surface, mais exiger de l'utilisateur qu'il traite cela par étapes séparées n'est pas efficace, en particulier lorsqu'un plus grand nombre de sections peut être nécessaire ou lorsque le positionnement précis des sections doit être trouvé de manière interactive. En X-Topologie, le processus est automatisé pour exposer une expérience de flux où le plan d'intersection est défini interactivement avec un certain nombre de clics de souris, la géométrie d'intersection et les nuages de points sont automatiquement sélectionnés et une courbe X-Topologie ajustée est générée directement à partir des coordonnées extraites. Les courbes peuvent être rapidement ajoutées et révisées interactivement après que le plan d'intersection est défini par le curseur de la souris.

Deux techniques d'ajustement de courbe sont mises en œuvre : la Spline Cubique, le Moindre Carré:

• L'ajustement spline génère une spline cubique qui interpole tous les points de coordonnées générés par l'intersection du plan. Il est significatif que le nombre de points de définition sur la courbe est directement lié au nombre de points d'intersection. C'est une caractéristique importante à garder à l'esprit lors de la génération de séquences de courbes qui devraient former une famille, c'est-à-dire qu'elles devraient avoir le même modèle mathématique pour éviter d'introduire une complexité inutile dans la surface générée à partir de nœuds supplémentaires et d'une paramétrisation incohérente qui sera perçue comme un défaut. De plus, le fait de garder le nombre de contrôles bas améliore la capacité de la forme juste et réduit le temps nécessaire pour garder une courbe juste. Il est préférable d'utiliser l'ajustement Spline pour générer des courbes secondaires qui traversent les courbes de conception principales et définissent les limites des patchs.

Un ajustement spline cubique utilisera chaque point échantillonné dans la définition de la courbe.

• L'ajustement des moindres carrés supprime le lien implicite entre le nombre de points d'intersection ou d'échantillonnage et le polygone de contrôle de la définition de la courbe ajustée. Le nombre de points de contrôle est un paramètre d'addition contrôlable par l'utilisateur. Il est possible d'introduire des fonctions de lissage qui peuvent améliorer la qualité de l'ajustement et soutenir la génération de points de contrôle lorsque les données sont limitées. La nécessité de revoir ces paramètres supplémentaires crée une pause dans le flux qui permet à l'utilisateur de jeter un second regard sur l'ajustement. Bien que cela puisse sembler contre-intuitif, l'expérience avec l'ajustement Spline suggère que les courbes d'intersection peuvent être ajoutées très rapidement en un seul clic et que souvent trop de courbes peuvent être ajoutées sans tenir compte de la qualité.

Dans les moindres carrés, le nombre de points de contrôle n'est pas lié au nombre de points d'échantillonnage et un carénage automatique est possible.

L'ajustement des moindres carrés est une méthode d'optimisation analytique qui présente de nombreuses similitudes avec le carénage[1] et la génération de courbes[2]. Les algorithmes pour l'ajustement des moindres carrés peuvent être trouvés dans de nombreux textes et la prémisse de base est la génération d'une courbe qui interpole un ensemble de points avec le moins d'erreur dans la distance au carré entre la courbe et les points. Le lissage introduit un ensemble supplémentaire d'équations qui réduisent la quantité d'énergie de flexion dans la courbe. En outre, des contraintes peuvent être ajoutées pour introduire des caractéristiques spécifiques dans la courbe. Les tangentes de courbe à la fin d'un segment ajusté doivent refléter l'information de tangente sur toute courbe X-Topologie à laquelle une connexion est faite. L'intersection avec la courbe X-Topologie avec la courbe d'information tangente divise la courbe en plusieurs segments qui sont ajustés indépendamment l'un de l'autre. Les courbes X-Topologie sans information tangente ne sont pas traitées en particulier et aucune tentative n'est faite pour interpoler ces courbes précisément parce que cela suggérerait que la courbe ajustée se comporte comme une courbe de conception secondaire plutôt que comme une courbe de conception primaire. Dans ces cas, un ajustement spline est mieux adapté.

Courbe échantillonnée à partir d'un nuage de points montrant l'écart relatif par rapport aux points échantillonnés.

Courbe échantillonnée à partir d'un nuage de points montrant la courbure.

Courbe échantillonnée à partir d'un nuage de points montrant la courbure avec lissage appliqué.

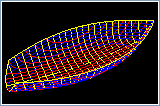
Courbes d'Ajustement et Topologie des Formes

L'un des défis de l'ajustement des courbes et des surfaces B-Spline aux points échantillonnés qui représente une forme avec des régions de différents degrés de courbure et des zones planes est qu'il est difficile pour l'algorithme d'ajustement d'adapter automatiquement la résolution du polygone de contrôle à la complexité de la forme. Les algorithmes d'ajustement espaceront normalement uniformément le polygone de contrôle, ce qui signifie que les zones de forte courbure sont sous- définies et les zones planes sur-définies. Généralement, les utilisateurs augmenteront le nombre de points de contrôle pour s'assurer que les zones à forte courbure sont représentées de façon adéquate, ce qui donne une définition ajustée qui a un nombre important de points de contrôle et qu'il est difficile de modifier à la main par la suite.

Informations de formes topologiques à partir de courbes avec des informations tangentes permettent de séparer l'ajustement à travers les différents types d'ajustement. Les régions de forme permetant d'utiliser le bon nombre de points au bon endroit.

Ce défi est atténué lorsque l'ajustement des courbes à un réseau de courbes X-Topologie existant qui contient la topologie des formes parce que les limites des différentes régions de forme sont capturées et peuvent diviser une courbe X-Topologie ajustée en plusieurs segments. Chaque segment est ajusté indépendamment, ce qui permet de sélectionner les paramètres d'ajustement optimaux pour cette région. Lorsqu'un segment est droit ou une courbe raccordée entre segments voisins, l'algorithme d'ajustement peut introduire les contraintes correspondantes de Courbe X-Topologie, évitant ainsi d'introduire des points de contrôle.​

Affiner les Réseaux de Courbes

Ce processus d'ajustement peut également être utilisé pour affiner le réseau de courbes X-Topologie pendant le processus de conception. Parfois, le réseau doit être réorganisé ou modifié pour améliorer sa forme ou s'adapter pour inclure une caractéristique. L'ajout de nouvelles courbes manuellement peut, dans le processus, endommager l'équité ou détruire la forme au fur et à mesure que vous adaptez la nouvelle géométrie. Le défi est que si vous n'ajoutez pas la nouvelle forme dans une position parfaite, certains changements seront vécus. Mais il est possible d'adapter une X-Topologie à une définition de surface à l'aide des outils d'ajustement de courbe. De plus, les outils comprennent cette exigence et référenceront automatiquement les courbes X-Topologie existantes à la nouvelle géométrie pour assurer la hiérarchie correcte entre les courbes de forme primaire et les courbes de croisement. Ce processus est démontré dans la vidéo ci-dessous.

Résumé

Réparer et reconstruire des surfaces en croisant des géométries efficaces génère des points sur lesquels des courbes et des surfaces peuvent être ajustées en évitant la numérisation manuelle. En incorporant les principes de la topologie des formes dans l'algorithme d'ajustement, les courbes X-Topologie peuvent être générées avec une définition sensible au degré de courbure de la géométrie originale et produire un polygone de contrôle qui peut être modifié à la main dans le cadre d'un processus de conception de surface.

Vous trouverez plus de détails sur le contexte du processus discuté sur cette page dans mon document COMPIT 2014. [3].

Références

1. Curves and Surfaces for CADG: A Practical Guide, G. Farin, 2002 , Morgan Kaufmann.
2. Computational Geometry for Ships, H. Nowacki, M.I.G. Bloor, B. Oleksiewicz, 1995, World Scientific Publishing Co Pte Ltd.
3. Regenerating Hull Design Definition from Poor Surface Definitions and other Geometric Representations, M.Bole, COMPIT 2014, Redworth, UK, 12-14 May 2014.