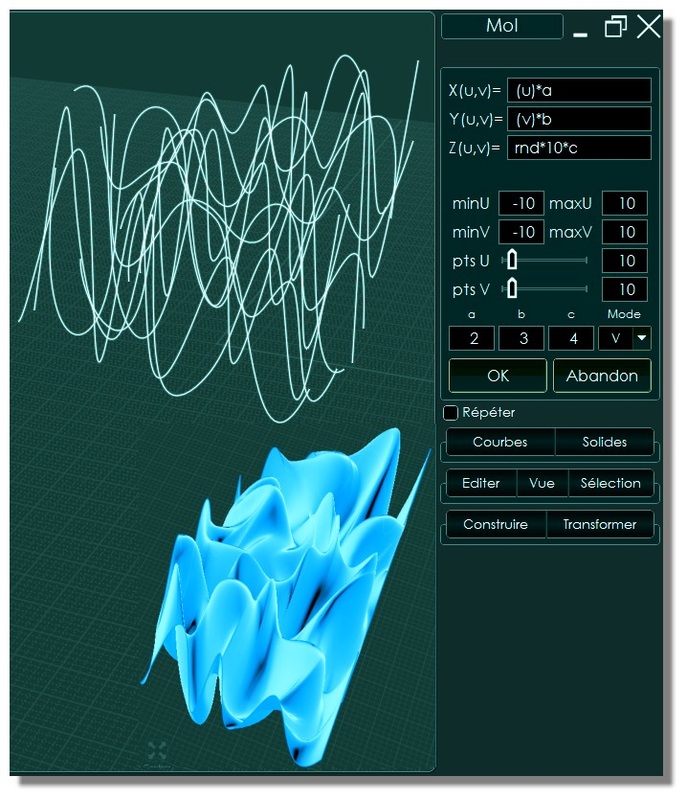
_FGraph3D: Entrer une fonction 3D à la volée pour la visualiser! By Smirnov
|
Post Original
Version française pas encore adaptée à la version nov 2017! Les fichiers _fxgraph3d décompressés sont à mettre dans le dossier commands. On peut appeler la commande par un raccourci ou par l'appui de la touche TAB! et taper au clavier _fxgraph3D (sans espace). Dans les colonnes des raccourcis. A _fxgraph3D Exemples de surfaces paramétriques! Si vous souhaitez utiliser des degrés au lieu de radians - utilisez des crochets. sin (x) <-- x en radians, sin [x] <-- x en degrés. Vous pouvez utiliser la commande "rnd" à la place de la fonction random () Cliquer sur X(u,v), Y(u,v) ou Z(u,v)...les copie dans le Presse-papiers. |
Autres paramètres:
minX, maxX - limites de la fonction. N'oubliez pas, dans Moi, vous pouvez utiliser un expression mathématique dans les paramètres.
Exemple: y = sin (x), minX = 0, maxX = 2 * pi <-- vous obtiendrez une période complète de la fonction sinusoïdale.
Points - nombre de points.
Si 50 points ne sont pas suffisant, vous pouvez définir une autre valeur manuellement.
Arguments de la ligne de commande
Usage: "_fxGraph3d fx;min;max;points;a;b;c;d"
Exemples:
_FxGraph3D a*c*sqrt(v)*cos(v);b*c*sqrt(v)*sin(v);0;0;1;0;6.283185307179586;0;50;1;1;1;UV
Copier la ligne du dessus, Presser TAb et la Coller!
Vous devriez obtenir une Spirale de Fermat!
Faire de même avec les fonctions suivantes!
_fxGraph3D sin(x) -> f(x)=sin(x)
_fxGraph3D sqrt(x);0;25 -> f(x)=sqrt(x), min(x)=0, max(x)=25
_fxGraph3D pow(x,a);;;;3 -> f(x)=pow(x,a), a=3
_FxGraph3D (u);(v);rnd;-10;10;-10;10;10;15;;;;U
_FxGraph3D u*a+rnd-0.5;v*b+rnd-0.5;rnd*c-c/2;-10;10;-10;10;50;50;2;2;40;P
_FxGraph3D 2*(1-exp(u/(6*pi)))*cos(u)*cos(v/2)*cos(v/2);2*(-1+exp(u/(6*pi)))*sin(u)*cos(v/2)*cos(v/2);1-exp(u/(3*pi))-sin(v)+exp(u/(6*pi))*sin(v);0;20;0;6.283185307179586;50;50;;;;V
_FxGraph3D (2+v*sin(u))*sin(2*pi*v);v*cos(u);(2+v*sin(u))*cos(2*pi*v)+2*v-v;0;3.14;0;1.3;50;50;;;;V
_FxGraph3D sin(u);cos(u);u*u/300;0;60;0;1.3;100;0;;;;V
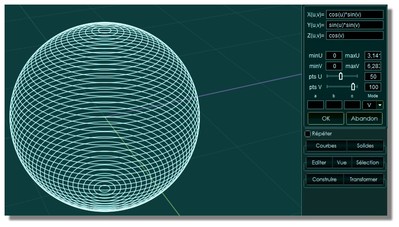
Sphère
_FxGraph3D cos(u)*cos(v)*a;sin(u)*cos(v)*b;sin(v)*c;0;6.283185307179586;-1.5707963267948966;1.5707963267948966;50;50;1;1;1;V
Tore
_FxGraph3D cos(u)*(cos(v)+a/b)*b;sin(u)*(cos(v)+a/b)*b;sin(v)*b;-3.141592653589793;3.141592653589793;-3.141592653589793;3.141592653589793;50;50;20;10;;UV
Spirale
_FxGraph3D cos(u/c)*(cos(v)+a/b)*b;sin(u/c)*(cos(v)+a/b)*b;sin(v)*b+u;0;50;0;6.283185307179586;100;20;10;3;2;UV
Spirale Conique
_FxGraph3D cos(u)*(u/(a*pi)*cos(v)+b)*c;sin(u)*(u/(a*pi)*cos(v)+b)*c;u*sin(v)/(a*pi)*c;0;9.42477796076938;0;6.283185307179586;100;20;1.5;5;1;U
Noeud
_FxGraph3D cos(u)*cos(v)+c*cos(u)*(b+sin(u*a)/2);sin(u)*cos(v)+c*sin(u)*(b+sin(a*u)/2);sin(v)+2*cos(a*u);0;18.84955592153876;0;6.283185307179586;300;10;1.666666;2;3;UV
Surface de Dini
_FxGraph3D cos(u)*sin(v);sin(u)*sin(v);cos(v)+log(tan(v/2))+a*u;0;12.566370614359172;0.1;2;300;10;0.3;;;U
Surface d'Ennneoper
_FxGraph3D u*cos(v)-pow(u,2*a-1)/(2*a-1)*cos((2*a-1)*v);-u*sin(v)-pow(u,2*a-1)/(2*a-1)*sin((2*a-1)*v);2/a*pow(u,a)*cos(a*v);0;1.2;0;6.283185307179586;50;27;4;;;UV
HyperbolicParaboloid1
_FxGraph3D u;v;u*v;-1;1;-1;1;50;50;0;0;0;UV
HyperbolicParaboloid2
_FxGraph3D a*(u+v);b*(u-v);u*v;-1;1;-1;1;50;50;1.618;1;0;UV
HyperbolicParaboloid3
_FxGraph3D (u);(v);c*((u*u)/(a*a) - (v*v)/(b*b));-1;1;-1;1;50;50;1.618;1;1;UV
HyperbolicParaboloid4
_FxGraph3D (u);(v)/(sqrt(1+a*a*u*u));v*a*u/(sqrt(1+a*a*u*u));-1;1;-1;1;50;50;1;1;1;UV
Coeur
_FxGraph3D a*16*sin(c*v)*sin(c*v)*sin(c*v);a*(13*cos(c*v)-5*cos(2*c*v)-2*cos(3*c*v)-cos(4*c*v));0;0;1;0;3.141592653589793;0;50;1;1;1;UV
sinhLeaf
_FxGraph3D u;v;((exp(u) - exp((-1)*u))/2 + (exp(v) - exp((-1)*v))/2);-3.14159;3.14159;-3.14159;3.14159;15;15;0;0;0;UV
sinhcoshScoop
_FxGraph3D u;v;((exp(u) - exp((-1)*u))/2 + (exp(v) + exp((-1)*v))/2);-3.14159;3.14159;-3.14159;3.14159;15;15;;;;UV
coshBag
_FxGraph3D u;v;((exp(u) + exp((-1)*u))/2 + (exp(v) + exp((-1)*v))/2);-3.14159;3.14159;-3.14159;3.14159;15;15;;;;UV
BowTie
_FxGraph3D v*sin(u);v*cos(u);a * asin(((exp(u*sin(v)) - exp(-u*sin(v)))/2) * ((exp(u*cos(v)) + exp(-u*cos(v)))/2));-0.8;0.8;-3.14159;3.14159;15;15;1;;;UV
Stereosphere
_FxGraph3D 2.*u/(u*u+v*v+1.);2.*v/(u*u+v*v+1.);(u*u+v*v-1.)/(u*u+v*v+1.);-2;2;-2;2;15;15;1;1;1;UV
Trompette
_FxGraph3D cos(u)*sin(v); sin(u)*sin(v); cos(v)+log(tan(1/2*v));0;6.283;0.03;1.5;50;50;1;1;1;UV
Fonctions admissibles
abs(x) Renvoie la valeur absolue de x
acos(x) Renvoie l'ArcCosinus de x, en radians
asin(x) Renvoie l'ArcSinus de x, en radians
atan(x) Renvoie l'ArcTangente de x comme une valeur numérique entre -PI/2 et PI/2 radians
ceil(x) Renvoie x, arrondis au plus proche entier supérieur
cos(x) Renvoie the Cosinus de x (x est en radians)
exp(x) Renvoie the valeur de l'exposant
floor(x) Renvoie x, arrondis au plus proche entier inférieur
log(x) Renvoie le logarithme naturel (base E) de x
pow(x,n) Renvoie la valeur de X puissance n
random() Renvoie un nombre aléatoire entre 0 et 1
round(x) Arrondit x au plus proche entier
sin(x) Renvoie le Sinus de x (x est en radians)
sqrt(x) Renvoie la racine carrée de x
tan(x) Renvoie la tangente d'un angle x
E Renvoie la constante d'Euler (environ 2.718)
LN2 Renvoie le logarithme naturel de 2 (environ 0.693)
LN10 Renvoie le logarithme naturel de 10 (environ 2.302)
LOG2E Renvoie Renvoie le logarithme base-2 de E (environ 1.442)
LOG10E Renvoie Renvoie le logarithme base-2 de E (environ 0.434)
PI Renvoie PI (environ 3.14)
SQRT1_2 Renvoie la racine carrée de 1/2 (environ 0.707)
SQRT2 Renvoie la racine carrée 2 (environ 1.414)
Le truc est de lancer le Script puis de prendre juste deux courbes pour faire une Surface Tendue ou un Tubage! C'est beaucoup plus rapide que de prendre toutes les courbes du résultat!