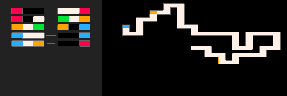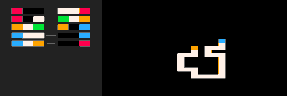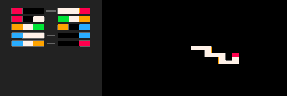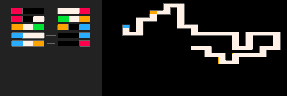MarkovJunior by Maxim Gumin Libre adaptation de l'Original
MarkovJunior est un langage de programmation probabiliste où les programmes sont des combinaisons de règles de réécriture et où l'inférence est effectuée par propagation de contraintes. MarkovJunior doit son nom au mathématicien Andrey Andreyevich Markov, qui a défini et étudié ce qu'on appelle aujourd'hui les algorithmes de Markov.
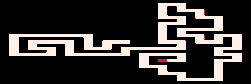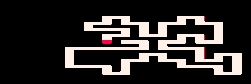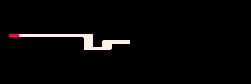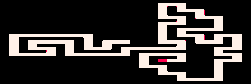
Dans sa forme de base, un programme MarkovJunior est une liste ordonnée de règles de réécriture. Par exemple, MazeBacktracker (animation à gauche ci-dessous) est une liste de 2 règles de réécriture :
RBB=GGR ou "remplacer rouge-noir-noir par vert-vert-rouge". (R=Red, B=Black, G=Green)
RGG=WWR ou "remplacer rouge-vert-vert par blanc-blanc-rouge" (W=White)
À chaque étape d'exécution, l'interpréteur MJ trouve la première règle de la liste qui a une correspondance sur la grille, trouve toutes les correspondances pour cette règle et applique cette règle pour une correspondance aléatoire. Dans l'exemple du backtracker du labyrinthe, l'interpréteur applique d'abord un tas de règles RBB=GGR. Mais finalement, la marche auto-évitante verte se bloque. À ce moment-là, la première règle n'a pas de correspondance, donc l'interpréteur applique la deuxième règle RGG=WWR jusqu'à ce que la marche se débloque. Ensuite, il peut à nouveau appliquer la première règle, et ainsi de suite. L'interpréteur s'arrête lorsqu'il n'y a plus de correspondance pour aucune règle.
RBB=GGR ou "remplacer rouge-noir-noir par vert-vert-rouge". (R=Red, B=Black, G=Green)
RGG=WWR ou "remplacer rouge-vert-vert par blanc-blanc-rouge" (W=White)
À chaque étape d'exécution, l'interpréteur MJ trouve la première règle de la liste qui a une correspondance sur la grille, trouve toutes les correspondances pour cette règle et applique cette règle pour une correspondance aléatoire. Dans l'exemple du backtracker du labyrinthe, l'interpréteur applique d'abord un tas de règles RBB=GGR. Mais finalement, la marche auto-évitante verte se bloque. À ce moment-là, la première règle n'a pas de correspondance, donc l'interpréteur applique la deuxième règle RGG=WWR jusqu'à ce que la marche se débloque. Ensuite, il peut à nouveau appliquer la première règle, et ainsi de suite. L'interpréteur s'arrête lorsqu'il n'y a plus de correspondance pour aucune règle.
L'inférence probabiliste dans MarkovJunior permet d'imposer des contraintes sur l'état futur, et de générer uniquement les exécutions qui mènent au futur contraint. Par exemple, l'inférence dans les règles de Sokoban {RWB=BRW RB=BR} fait qu'un groupe d'agents (rouges) organise des caisses (blanches) dans des formes spécifiées.
En utilisant ces idées, nous construisons de nombreux générateurs probabilistes de donjons, d'architecture, de puzzles et de simulations amusantes.
En utilisant ces idées, nous construisons de nombreux générateurs probabilistes de donjons, d'architecture, de puzzles et de simulations amusantes.
Captures d'écran en plus haute résolution et plus de graines : ModernHouse, SeaVilla, Apartemazements, CarmaTower, Escheresque, PillarsOfEternity, Surface, Knots.
Algorithmes de Markov
Un algorithme de Markov sur un alphabet A est une liste ordonnée de règles. Chaque règle est une chaîne de la forme x=y, où x et y sont des mots dans A, et certaines règles peuvent être marquées comme des règles d'arrêt. L'application d'un algorithme de Markov à un mot w se déroule comme suit :
1=0x
x0=0xx
0=ε
Si on l'applique à la chaîne 110, on obtient cette séquence de chaînes :
110 -> 0x10 -> 0x0x0 -> 00xxx0 -> 00xx0xx -> 00x0xxxx -> 000xxxxxx -> 00xxxxxx -> 0xxxxxx -> xxxxxx.
En général, cet algorithme convertit la représentation binaire d'un nombre en sa représentation unaire.
Un algorithme de Markov sur un alphabet A est une liste ordonnée de règles. Chaque règle est une chaîne de la forme x=y, où x et y sont des mots dans A, et certaines règles peuvent être marquées comme des règles d'arrêt. L'application d'un algorithme de Markov à un mot w se déroule comme suit :
- Trouver la première règle x=y où x est une sous-chaîne de w. S'il n'y a pas de telles règles, alors on s'arrête.
- Remplacer le x le plus à gauche de w par y.
- Si la règle trouvée est une règle d'arrêt, alors arrêtez-vous. Sinon, passer à l'étape 1.
1=0x
x0=0xx
0=ε
Si on l'applique à la chaîne 110, on obtient cette séquence de chaînes :
110 -> 0x10 -> 0x0x0 -> 00xxx0 -> 00xx0xx -> 00x0xxxx -> 000xxxxxx -> 00xxxxxx -> 0xxxxxx -> xxxxxx.
En général, cet algorithme convertit la représentation binaire d'un nombre en sa représentation unaire.
Vilnis Detlovs, étudiant de Markov, a prouvé que pour toute machine de Turing, il existe un algorithme de Markov qui calcule la même fonction. En comparaison, les grammaires sont des ensembles non ordonnés de règles de réécriture et les systèmes L sont des règles de réécriture qui sont appliquées en parallèle. Pour d'autres exemples intéressants d'algorithmes de Markov, consultez le livre de Markov ou voyez l'exemple du plus grand diviseur commun dans la section des commentaires ou l'exemple de la multiplication sur Wikipedia.
Comment généraliser les algorithmes de Markov à plusieurs dimensions ? Tout d'abord, en dimensions multiples, il n'y a pas de moyens naturels d'insérer une chaîne dans une autre chaîne, de sorte que les gauches et les droits de nos règles de réécriture devraient avoir la même taille. Deuxièmement, il n'existe pas de moyens naturels de choisir la correspondance la plus à gauche. Les options possibles sont les suivantes :
Choisir une correspondance aléatoire. C'est ce que font les nœuds (existants) de MJ.
Choisir toutes les correspondances. Il y a un problème avec cette option cependant parce que différentes correspondances peuvent se chevaucher et avoir des conflits. Les solutions possibles sont :
Choisir avec avidité un sous-ensemble maximal de correspondances non conflictuelles. C'est ce que font les noeuds {forall} de MJ.
Considérer toutes les correspondances en superposition. C'est-à-dire qu'au lieu de valeurs séparées, gardez des ondes dans chaque cellule de la grille - des vecteurs booléens qui indiquent quels modèles spatio-temporels sont interdits et lesquels ne le sont pas. Et c'est ainsi que MJ effectue l'inférence.
Nous perdons la complétude de Turing parce que notre nouvelle procédure n'est pas déterministe, mais la pratique montre que ce formalisme permet toujours de décrire un large éventail de processus aléatoires intéressants.
Comment généraliser les algorithmes de Markov à plusieurs dimensions ? Tout d'abord, en dimensions multiples, il n'y a pas de moyens naturels d'insérer une chaîne dans une autre chaîne, de sorte que les gauches et les droits de nos règles de réécriture devraient avoir la même taille. Deuxièmement, il n'existe pas de moyens naturels de choisir la correspondance la plus à gauche. Les options possibles sont les suivantes :
Choisir une correspondance aléatoire. C'est ce que font les nœuds (existants) de MJ.
Choisir toutes les correspondances. Il y a un problème avec cette option cependant parce que différentes correspondances peuvent se chevaucher et avoir des conflits. Les solutions possibles sont :
Choisir avec avidité un sous-ensemble maximal de correspondances non conflictuelles. C'est ce que font les noeuds {forall} de MJ.
Considérer toutes les correspondances en superposition. C'est-à-dire qu'au lieu de valeurs séparées, gardez des ondes dans chaque cellule de la grille - des vecteurs booléens qui indiquent quels modèles spatio-temporels sont interdits et lesquels ne le sont pas. Et c'est ainsi que MJ effectue l'inférence.
Nous perdons la complétude de Turing parce que notre nouvelle procédure n'est pas déterministe, mais la pratique montre que ce formalisme permet toujours de décrire un large éventail de processus aléatoires intéressants.
Règles de réécriture
Le programme de MarkovJunior le plus simple est probablement (B=W). Il ne contient qu'une seule règle B=W. À chaque tour, ce programme convertit un carré noir aléatoire en un carré blanc.
Le programme de MarkovJunior le plus simple est probablement (B=W). Il ne contient qu'une seule règle B=W. À chaque tour, ce programme convertit un carré noir aléatoire en un carré blanc.
(B=W) | (WB=WW) | (WBB=WAW) | (WBB=WAW)
Le modèle de croissance (WB=WW) est plus intéressant. À chaque tour, il remplace une paire noire-blanche de cellules adjacentes BW par une paire blanche-blanche WW. En d'autres termes, à chaque tour, il choisit au hasard une cellule noire adjacente à une cellule blanche et la colore en blanc. Ce modèle est presque identique au modèle de croissance Eden : à chaque tour, les deux modèles choisissent parmi le même ensemble de cellules noires. Ils ne diffèrent que par leurs distributions de probabilité : une distribution uniforme sur les cellules noires adjacentes à des cellules blanches n'est pas la même qu'une distribution uniforme sur les paires de cellules noires et blanches adjacentes.
Le modèle (WBB=WAW) génère un labyrinthe, avec une seule ligne de code ! Comparez-le avec une implémentation dans un langage conventionnel. Tout modèle MarkovJunior peut être exécuté dans n'importe quel nombre de dimensions sans modifications. A droite, vous pouvez voir le résultat final de MazeGrowth en 3d, rendu en MagicaVoxel. Par défaut, nous utilisons la palette PICO-8 :
Le modèle (WBB=WAW) génère un labyrinthe, avec une seule ligne de code ! Comparez-le avec une implémentation dans un langage conventionnel. Tout modèle MarkovJunior peut être exécuté dans n'importe quel nombre de dimensions sans modifications. A droite, vous pouvez voir le résultat final de MazeGrowth en 3d, rendu en MagicaVoxel. Par défaut, nous utilisons la palette PICO-8 :
Le modèle (RBB=WWWR) est une marche aléatoire auto-évitante. Notez que les marches auto-évitantes en 3d sont en moyenne plus longues qu'en 2d. En général, la comparaison des comportements de processus aléatoires similaires dans différentes dimensions est un sujet fascinant. Un résultat classique de George Pólya indique qu'une marche aléatoire en 2d revient à sa position initiale avec une probabilité de un, alors qu'en 3d ce n'est plus le cas.
(RBB=WWR) | Marche en Boucles Effaçantes | (RB=WR RW=WR)
On peut mettre plusieurs règles dans un seul nœud de règle. Par exemple, (RBB=WWR RBW=GWP PWG=PBU UWW=BBU UWP=BBR) est une marche aléatoire avec boucle. Le modèle de parcours (RB=WR RW=WR) génère des grottes connectées décentes.
Le modèle (RBB=WWR R*W=W*R) est connu comme l'algorithme de génération de labyrinthes d'Aldous-Broder. Le symbole joker * dans l'entrée signifie que n'importe quelle couleur est autorisée à se trouver dans le carré. Le symbole joker en sortie signifie que la couleur ne change pas après l'application de la règle.
L'algorithme d'Aldous-Broder prend en moyenne beaucoup plus de tours pour générer un labyrinthe que MazeGrowth, par exemple, mais il possède une propriété intéressante que MazeGrowth n'a pas : chaque labyrinthe a la même probabilité d'être généré. En d'autres termes, MazeTrail est un algorithme de génération de labyrinthes sans biais, c'est-à-dire qu'il échantillonne les labyrinthes (ou les arbres spanning) avec une distribution uniforme. L'algorithme de Wilson est un algorithme de génération de labyrinthes sans biais plus efficace. Comparez son implémentation dans MarkovJunior avec une implémentation dans un langage conventionnel !
Le modèle (RBB=WWR R*W=W*R) est connu comme l'algorithme de génération de labyrinthes d'Aldous-Broder. Le symbole joker * dans l'entrée signifie que n'importe quelle couleur est autorisée à se trouver dans le carré. Le symbole joker en sortie signifie que la couleur ne change pas après l'application de la règle.
L'algorithme d'Aldous-Broder prend en moyenne beaucoup plus de tours pour générer un labyrinthe que MazeGrowth, par exemple, mais il possède une propriété intéressante que MazeGrowth n'a pas : chaque labyrinthe a la même probabilité d'être généré. En d'autres termes, MazeTrail est un algorithme de génération de labyrinthes sans biais, c'est-à-dire qu'il échantillonne les labyrinthes (ou les arbres spanning) avec une distribution uniforme. L'algorithme de Wilson est un algorithme de génération de labyrinthes sans biais plus efficace. Comparez son implémentation dans MarkovJunior avec une implémentation dans un langage conventionnel !
Combinaison de Nœuds de Règles
Nous pouvons placer plusieurs Nœuds de Règles dans un nœud de séquence, à exécuter l'un après l'autre. Dans le modèle de rivière, nous construisons d'abord un diagramme de Voronoï stochastique avec 2 sources, et utilisons la frontière entre les régions formées comme base pour une rivière. Ensuite, nous faisons naître quelques graines de Voronoï supplémentaires pour faire pousser des forêts et simultanément de l'herbe à partir de la rivière. Nous obtenons ainsi des vallées fluviales aléatoires !
Nous pouvons placer plusieurs Nœuds de Règles dans un nœud de séquence, à exécuter l'un après l'autre. Dans le modèle de rivière, nous construisons d'abord un diagramme de Voronoï stochastique avec 2 sources, et utilisons la frontière entre les régions formées comme base pour une rivière. Ensuite, nous faisons naître quelques graines de Voronoï supplémentaires pour faire pousser des forêts et simultanément de l'herbe à partir de la rivière. Nous obtenons ainsi des vallées fluviales aléatoires !
Dans Apartemazements, nous commençons par un nœud WFC, puis nous effectuons un post-traitement constructif avec des nœuds de règles :
Une façon plus intéressante de combiner des noeuds est de les mettre dans un Noeud de Markov. Les nœuds de Markov étendent considérablement ce que nous pouvons faire, car ils permettent de revenir aux nœuds précédents. Lorsqu'un Noeud de Markov est actif, l'interpréteur trouve son premier noeud enfant qui correspond et l'applique. Au tour suivant, il trouve à nouveau le premier nœud correspondant dans la liste, et ainsi de suite. L'exemple le plus simple de l'utilisation des Nœuds de Markov est le MazeBacktracker expliqué dans la section supérieure.
- Préparez les contraintes : marquez les cellules de fond avec une couleur de fond distincte, marquez les cellules de bordure restantes (côtés et haut) avec une couleur de bordure distincte. Les cellules de bordure doivent correspondre à Empty, les cellules du bas doivent correspondre à toutes les tuiles sauf Down.
- Exécutez le jeu de tuiles WFC Paths pour générer des cycles fermés en escalier.
- Randomisez les sources de lumière.
- Déposer les colonnes des coins des tuiles plates.
- Rétracter les colonnes doubles, les colonnes qui touchent le sol et les colonnes qui touchent les escaliers, sauf les colonnes qui poussent depuis les coins des tuiles Turn.
- Faire grandir les fenêtres entre les colonnes voisines.
- Fusionner les fenêtres dans des rectangles plus grands. Nous faisons cela en plusieurs étapes :
- Détecter les motifs irréguliers des fenêtres lorsque les coins des fenêtres touchent les points médians des fenêtres.
- Marquer ces motifs et propager les marquages sur toute la longueur des côtés de la fenêtre.
- Fusionner les paires de côtés de fenêtres non marquées.
Une façon plus intéressante de combiner des noeuds est de les mettre dans un Noeud de Markov. Les nœuds de Markov étendent considérablement ce que nous pouvons faire, car ils permettent de revenir aux nœuds précédents. Lorsqu'un Noeud de Markov est actif, l'interpréteur trouve son premier noeud enfant qui correspond et l'applique. Au tour suivant, il trouve à nouveau le premier nœud correspondant dans la liste, et ainsi de suite. L'exemple le plus simple de l'utilisation des Nœuds de Markov est le MazeBacktracker expliqué dans la section supérieure.
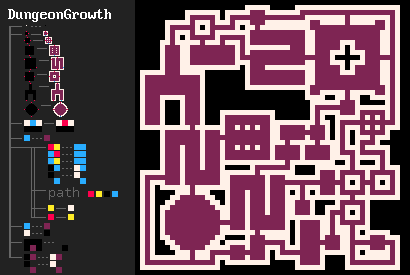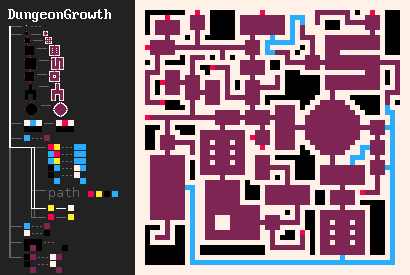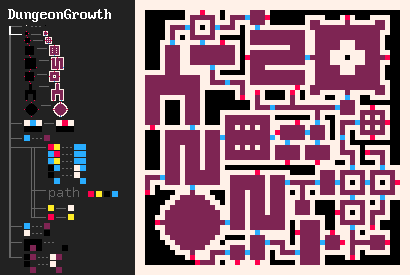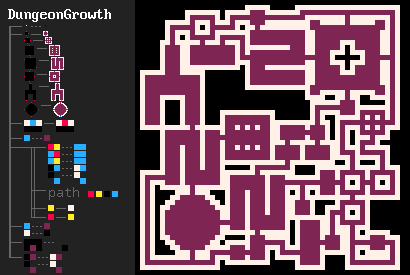
L'un de mes exemples favoris qui a motivé le développement de MarkovJunior est l'algorithme de génération de donjons de Bob Nystrom. Il se déroule comme suit :
- Dessiner une grille {PBB=**P}.
- Créer une série de pièces (room.png).
- Générer un labyrinthe sur le reste de la grille. Nous pouvons utiliser n'importe quel algorithme de génération de labyrinthe, mais MazeBacktracker est préféré car il produit moins de points de branchement.
- Faire en sorte que la configuration résultante de pièces et de couloirs soit connectée. Cela peut être fait de manière élégante avec un Nœud de Markov ({GWW=**G}(GBW=*WG)).
- Effectuez quelques connexions supplémentaires (GBG=*W* #5), afin que le donjon résultant ait des cycles. Les donjons sans cycles sont assez ennuyeux, car le joueur doit revenir par des zones déjà explorées.
- Retirez les impasses {BBB/BWB=BBB/BBB}.
Comme dans REFAL, les Nœuds de Markov peuvent être imbriqués : une fois que nous entrons dans un nœud enfant, nous ignorons les nœuds extérieurs jusqu'à ce que la branche enfant soit terminée.
Inférence
L'inférence probabiliste dans MarkovJunior permet d'imposer des contraintes sur l'état futur, et de générer uniquement les exécutions qui mènent au futur contraint. En d'autres termes, l'inférence connecte 2 états donnés (ou des états partiellement observés) avec une chaîne de règles de réécriture.
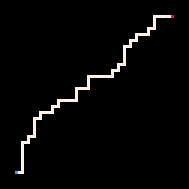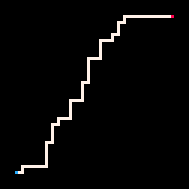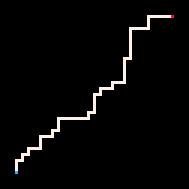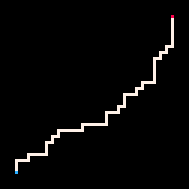
L'exemple le plus simple d'utilisation de l'inférence est la connexion de deux points par un chemin. Dans le modèle de la marche auto-évitante (RBB=WWR), nous pouvons observer qu'un carré donné sur la grille devient rouge R. L'interpréteur ne génère alors que les marches qui mènent au carré observé. Nous pouvons faire en sorte que l'interpréteur suive le but plus ou moins strictement en faisant varier le paramètre de température. Par défaut, la température est fixée à zéro.
L'inférence probabiliste dans MarkovJunior permet d'imposer des contraintes sur l'état futur, et de générer uniquement les exécutions qui mènent au futur contraint. En d'autres termes, l'inférence connecte 2 états donnés (ou des états partiellement observés) avec une chaîne de règles de réécriture.
L'exemple le plus simple d'utilisation de l'inférence est la connexion de deux points par un chemin. Dans le modèle de la marche auto-évitante (RBB=WWR), nous pouvons observer qu'un carré donné sur la grille devient rouge R. L'interpréteur ne génère alors que les marches qui mènent au carré observé. Nous pouvons faire en sorte que l'interpréteur suive le but plus ou moins strictement en faisant varier le paramètre de température. Par défaut, la température est fixée à zéro.
Le Plus froid | Froid | Chaud | Le plus chaud
Une autre chose que nous pouvons faire est d'observer toutes les cases impaires de la grille devenir blanches ou rouges. L'interpréteur génère alors des marches auto-évitantes qui couvrent la totalité de la grille.
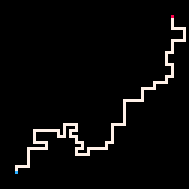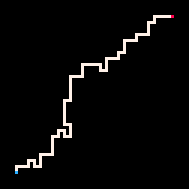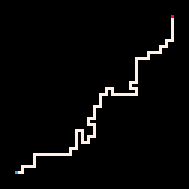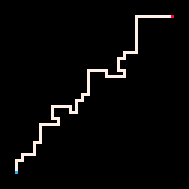
Nous pouvons engager l'inférence pour n'importe quelle règle de réécriture. Par exemple, l'inférence pour les règles de réécriture en escalier relie 2 points avec un chemin en escalier. L'inférence pour la règle R**/**B=B**/**R génère des chemins qu'un cavalier d'échecs peut emprunter. L'inférence pour le modèle CrossCountry connecte 2 points avec un chemin prenant en compte les coûts du terrain. L'inférence pour l'ensemble de règles Sokoban {RB=BR RWB=BRW} résout des puzzles Sokoban ou même des puzzles Sokoban multi-agents !
L'inférence dans MarkovJunior se fait par propagation de contraintes unidirectionnelle (rapide) ou bidirectionnelle (lente, mais plus puissante). La propagation unidirectionnelle des contraintes pour les règles de réécriture peut être décrite de manière équivalente en termes de champs de propagation de règles qui généralisent les champs de Dijkstra pour les règles de réécriture arbitraires. Les champs de Dijkstra sont une technique populaire dans la génération procédurale basée sur la grille (1, 2, 3). Ils généralisent à leur tour les champs de distance utilisés en infographie.
Si la propagation des contraintes est terminée, cela ne signifie pas nécessairement que l'état cible est réalisable. Mais si la propagation échoue, nous savons avec certitude que le but n'est pas réalisable. Cela permet d'attraper les états où une caisse est poussée vers le mauvais mur dans Sokoban, ou lorsque la marche de couverture de la grille divise la grille en deux parties déconnectées. En plus de cette heuristique booléenne, il est intéressant de regarder le nombre minimal de tours nécessaires pour que la propagation des contraintes soit complète. Cette heuristique à valeurs entières est admissible, et nous l'utilisons dans la recherche A* pour échantillonner les chemins constitués de règles de réécriture entre 2 états donnés.
Si la propagation des contraintes est terminée, cela ne signifie pas nécessairement que l'état cible est réalisable. Mais si la propagation échoue, nous savons avec certitude que le but n'est pas réalisable. Cela permet d'attraper les états où une caisse est poussée vers le mauvais mur dans Sokoban, ou lorsque la marche de couverture de la grille divise la grille en deux parties déconnectées. En plus de cette heuristique booléenne, il est intéressant de regarder le nombre minimal de tours nécessaires pour que la propagation des contraintes soit complète. Cette heuristique à valeurs entières est admissible, et nous l'utilisons dans la recherche A* pour échantillonner les chemins constitués de règles de réécriture entre 2 états donnés.
Problèmes ouverts
1. Synthèse de programme pour la génération procédurale. La présentation de William Chyr "Level Design in Impossible Geometry" n'est pas du tout sur la génération procédurale, pourtant je trouve une diapositive très caractéristique pour la pratique du pcg. William compare ses approches précédentes et ultérieures de la conception de niveaux. La première produisait des niveaux chaotiques, tandis que la dernière approche produisait des niveaux plus structurés, plus intentionnels, basés sur une idée centrale. Les niveaux ultérieurs n'étaient pas plus simples, mais ils étaient plus mémorables et plus faciles à percevoir pour les joueurs. Pour moi, le niveau de gauche semble avoir été généré de manière procédurale ! Il ressemble beaucoup à mes puzzles voxels procéduraux. Peut-on créer des générateurs qui produisent des niveaux ressemblant davantage à celui de droite ? Ce problème peut sembler complet du point de vue de l'IA. Mais je dirais qu'il est très similaire aux problèmes classiques de programmation génétique comme le problème de la tondeuse à gazon de Koza. Par exemple, prenez une simple tâche de procgen consistant à générer des chemins hamiltoniens sur la grille. Même pour des grilles de petite taille, comme 29x29, cette tâche est déjà exigeante sur le plan informatique. Mais avons-nous vraiment besoin d'échantillonner tous les chemins possibles en pratique ? Si nous confions cette tâche à un être humain, il dessinera probablement une spirale ou une courbe en zigzag - ces dessins sont beaucoup plus mémorables et intentionnels qu'un chemin hamiltonien aléatoire, et ils se généralisent à toutes les tailles de grille. En résumé, nous pouvons demander au système soit de trouver un chemin hamiltonien aléatoire, soit de trouver un programme court qui génère des chemins hamiltoniens. Dans le premier cas, le résultat ressemblerait au niveau gauche de la diapositive, et dans le second cas, au niveau droit. Résoudre ce dernier problème de synthèse de programme permettrait de créer des générateurs plus mémorables et plus intentionnels.
2. Synthèse de modèles à partir d'exemples. Les algorithmes de Markov semblent être un environnement parfait pour la synthèse de programmes/modèles : pas de variables, de "si" ou de "whiles", les nœuds peuvent être facilement déplacés sans que cela n'affecte la correction, les modèles sont faciles à rendre différentiables. Les programmes MJ aléatoires sont souvent amusants et peuvent produire des résultats et des comportements comparables à ceux de l'homme.
3. Algorithmes personnalisés qui s'exécutent dans l'espace des ondes. Réunir les avantages de la génération procédurale constructive et basée sur des contraintes. Connexe : algorithmes personnalisés (règles de réécriture MJ) avec des fonctions d'énergie personnalisées comme l'énergie Ising ou l'énergie ConvChain.
4. Généraliser la notion de motif.
5. Étudier les processus de type MJ sur d'autres grilles (éventuellement non régulières) ou sur des graphes arbitraires.
6. Expérimenter des extensions interactives des algorithmes de Markov. Il est possible de transformer n'importe quel modèle MJ en un jeu en assignant des règles de réécriture ou des nœuds spécifiques aux pressions de touches.
7. Repousser les limites de l'état de l'art en matière de génération procédurale basée sur des grilles. ModernHouse n'atteint pas encore la variété structurelle des maisons conçues par des humains, comme celles des Sims 2. Utilisez des contraintes plus subtiles.
1. Synthèse de programme pour la génération procédurale. La présentation de William Chyr "Level Design in Impossible Geometry" n'est pas du tout sur la génération procédurale, pourtant je trouve une diapositive très caractéristique pour la pratique du pcg. William compare ses approches précédentes et ultérieures de la conception de niveaux. La première produisait des niveaux chaotiques, tandis que la dernière approche produisait des niveaux plus structurés, plus intentionnels, basés sur une idée centrale. Les niveaux ultérieurs n'étaient pas plus simples, mais ils étaient plus mémorables et plus faciles à percevoir pour les joueurs. Pour moi, le niveau de gauche semble avoir été généré de manière procédurale ! Il ressemble beaucoup à mes puzzles voxels procéduraux. Peut-on créer des générateurs qui produisent des niveaux ressemblant davantage à celui de droite ? Ce problème peut sembler complet du point de vue de l'IA. Mais je dirais qu'il est très similaire aux problèmes classiques de programmation génétique comme le problème de la tondeuse à gazon de Koza. Par exemple, prenez une simple tâche de procgen consistant à générer des chemins hamiltoniens sur la grille. Même pour des grilles de petite taille, comme 29x29, cette tâche est déjà exigeante sur le plan informatique. Mais avons-nous vraiment besoin d'échantillonner tous les chemins possibles en pratique ? Si nous confions cette tâche à un être humain, il dessinera probablement une spirale ou une courbe en zigzag - ces dessins sont beaucoup plus mémorables et intentionnels qu'un chemin hamiltonien aléatoire, et ils se généralisent à toutes les tailles de grille. En résumé, nous pouvons demander au système soit de trouver un chemin hamiltonien aléatoire, soit de trouver un programme court qui génère des chemins hamiltoniens. Dans le premier cas, le résultat ressemblerait au niveau gauche de la diapositive, et dans le second cas, au niveau droit. Résoudre ce dernier problème de synthèse de programme permettrait de créer des générateurs plus mémorables et plus intentionnels.
2. Synthèse de modèles à partir d'exemples. Les algorithmes de Markov semblent être un environnement parfait pour la synthèse de programmes/modèles : pas de variables, de "si" ou de "whiles", les nœuds peuvent être facilement déplacés sans que cela n'affecte la correction, les modèles sont faciles à rendre différentiables. Les programmes MJ aléatoires sont souvent amusants et peuvent produire des résultats et des comportements comparables à ceux de l'homme.
- Peut-on synthétiser un modèle MJ à partir d'un résultat ou d'un ensemble de résultats ?
- Étant donné un labyrinthe, est-il possible de déterminer (ou d'attribuer des probabilités) s'il a été généré par MazeGrowth ou MazeBacktracker ?
- Résolvez le défi de l'abstraction et du raisonnement en déduisant des modèles Markov-Junior. Problème d'adjonction : utilisez les connaissances acquises dans le cadre du défi ARC pour construire un meilleur DSL pour la génération procédurale sur une grille.
3. Algorithmes personnalisés qui s'exécutent dans l'espace des ondes. Réunir les avantages de la génération procédurale constructive et basée sur des contraintes. Connexe : algorithmes personnalisés (règles de réécriture MJ) avec des fonctions d'énergie personnalisées comme l'énergie Ising ou l'énergie ConvChain.
4. Généraliser la notion de motif.
5. Étudier les processus de type MJ sur d'autres grilles (éventuellement non régulières) ou sur des graphes arbitraires.
6. Expérimenter des extensions interactives des algorithmes de Markov. Il est possible de transformer n'importe quel modèle MJ en un jeu en assignant des règles de réécriture ou des nœuds spécifiques aux pressions de touches.
7. Repousser les limites de l'état de l'art en matière de génération procédurale basée sur des grilles. ModernHouse n'atteint pas encore la variété structurelle des maisons conçues par des humains, comme celles des Sims 2. Utilisez des contraintes plus subtiles.
Commentaires
Comparé aux machines de Turing et au lambda calculus, l'algorithme de Markov est probablement le moyen le plus court et le plus simple de définir rigoureusement ce qu'est un algorithme.
Exercice : prouver que l'algorithme de Markov suivant trouve le plus grand diviseur commun de 2 nombres écrits dans une représentation unaire. Par exemple, si on l'applique à 111111*111111111111 on obtient 11.
1a=a1
1*1=a*
1*=*b
b=1
a=c
c=1
*=ε (arrêt)
Correspondance rapide de motifs. L'interpréteur MarkovJunior échantillonne les correspondances uniformément, mais il ne scanne pas toute la grille à chaque tour. Pour que le filtrage soit rapide, l'interpréteur se souvient des correspondances précédemment trouvées et ne cherche qu'aux endroits qui ont été modifiés. Quand un Nœud de règle est rencontré pour la première fois, l'interpréteur MJ utilise une version multidimensionnelle de l'algorithme de Boyer-Moore.
Relaxation stochastique. Les nœuds de Markov ont une représentation très agréable en tant que limites de nœuds différentiables. Considérons un ensemble non ordonné de règles de réécriture où chaque règle r se voit attribuer un poids w(r). À chaque étape, l'interprète trouve toutes les correspondances pour toutes les règles et choisit une correspondance aléatoire selon la distribution de Boltzmann p(r) ~ exp(-w(r)/t). Ensuite, dans la limite de congélation t->0, nous obtenons un nœud de Markov, ordonné par les poids. Ce qui est bien dans cette construction, c'est que pour n'importe quel t>0 et pour une fonction de score typique, la moyenne du score sur plusieurs passages serait une fonction continue (et lisse pour des raisons pratiques) des poids. Cela signifie que l'on peut trouver les poids optimaux par descente de gradient, puis geler le système pour obtenir le programme discret final.
Lisez cet essai de Boris Kushner sur A. A. Markov et son travail en mathématiques constructives.
Comparé aux machines de Turing et au lambda calculus, l'algorithme de Markov est probablement le moyen le plus court et le plus simple de définir rigoureusement ce qu'est un algorithme.
Exercice : prouver que l'algorithme de Markov suivant trouve le plus grand diviseur commun de 2 nombres écrits dans une représentation unaire. Par exemple, si on l'applique à 111111*111111111111 on obtient 11.
1a=a1
1*1=a*
1*=*b
b=1
a=c
c=1
*=ε (arrêt)
Correspondance rapide de motifs. L'interpréteur MarkovJunior échantillonne les correspondances uniformément, mais il ne scanne pas toute la grille à chaque tour. Pour que le filtrage soit rapide, l'interpréteur se souvient des correspondances précédemment trouvées et ne cherche qu'aux endroits qui ont été modifiés. Quand un Nœud de règle est rencontré pour la première fois, l'interpréteur MJ utilise une version multidimensionnelle de l'algorithme de Boyer-Moore.
Relaxation stochastique. Les nœuds de Markov ont une représentation très agréable en tant que limites de nœuds différentiables. Considérons un ensemble non ordonné de règles de réécriture où chaque règle r se voit attribuer un poids w(r). À chaque étape, l'interprète trouve toutes les correspondances pour toutes les règles et choisit une correspondance aléatoire selon la distribution de Boltzmann p(r) ~ exp(-w(r)/t). Ensuite, dans la limite de congélation t->0, nous obtenons un nœud de Markov, ordonné par les poids. Ce qui est bien dans cette construction, c'est que pour n'importe quel t>0 et pour une fonction de score typique, la moyenne du score sur plusieurs passages serait une fonction continue (et lisse pour des raisons pratiques) des poids. Cela signifie que l'on peut trouver les poids optimaux par descente de gradient, puis geler le système pour obtenir le programme discret final.
Lisez cet essai de Boris Kushner sur A. A. Markov et son travail en mathématiques constructives.
Travaux
Principal ouvrage utilisé :
- Andrey A. Markov, The Theory of Algorithms, 1951. Markov a utilisé ces idées plus tôt en 1947 dans sa preuve de l'indécidabilité algorithmique du problème des mots dans les semi-groupes. Voir aussi un livre ultérieur avec un traitement plus détaillé. Je serais reconnaissant pour les liens vers les traductions anglaises en accès libre.
- Guilherme S. Tows, Imagegram, 2009. MarkovJunior prend forall-nodes d'Imagegram.
- Valentin Turchin, langage REFAL, 1968. MJ prend l'idée de nœuds de Markov imbriqués de REFAL.
- Brian Walker et al, The incredible power of Dijkstra maps, 2010. Une discussion dans la communauté roguelike qui contient de nombreuses techniques d'utilisation des cartes de Dijkstra/champs de distance pour la génération de procédures et l'IA des PNJ. Écrits plus tard : 1, 2. Nous généralisons les cartes de Dijkstra aux règles de réécriture arbitraires.
- Pavlos S. Efraimidis, Paul Spirakis, Weighted Random Sampling, 2005.
- Travaux utilisés dans les nœuds personnalisés : Model Synthesis, Wave Function Collapse Algorithm, ConvChain Algorithm.
- Algorithmes classiques : constraint propagation, constraint solving algorithms, graph traversal, A* search.
Travaux connexes :
Sources des exemples :
Les scènes Voxel ont été rendues dans MagicaVoxel par ephtracy. Des remerciements particuliers à Brian Bucklew pour m'avoir démontré la puissance des champs de Dijkstra dans la génération de niveaux de roguelike et à Kevin Chapelier pour un certain nombre de bonnes suggestions. La police utilisée dans l'interface graphique est Tamzen...
- BasicKeys et Keys sont des adaptations de grammaires de graphes formulées par Joris Dormans, Engineering Emergence: Applied Theory for Game Design , 2012. Qui sont à leur tour un développement du travail antérieur de David Adams, Automatic Generation of Dungeons for Computer Games, 2002. J'utilise une variante de ces modèles pour générer des énigmes de type clé-lock-pont dans SeaVilla.
- CarmaTower est une procéduralisation d'une scène voxel d'Antoine Lendrevie.
- Le modèle NystromDungeon est un portage MarkovJunior du générateur de donjons de Bob Nystrom.
- L'algorithme HamiltonianPath est adapté de cet article. Comparez-le avec une implémentation dans un langage conventionnel.
- Les formes des pièces dans DungeonGrowth sont tirées du post r/proceduralgeneration. Notez que l'interpréteur MJ effectue automatiquement les optimisations décrites dans le post.
- Le modèle Wilson est une formulation des règles de réécriture de l'algorithme de Wilson. Comparez-le avec une implémentation dans un langage conventionnel.
- Le modèle MazeGrowth est également connu sous le nom de génération de labyrinthes par traversée aléatoire. Comparez-le avec une mise en œuvre dans un langage conventionnel.
- Le modèle Growth est étroitement lié au modèle de croissance d'Eden.
- BernoulliPercolation est un modèle bien étudié dans une théorie de percolation.
- NestedGrowth est tiré de Imagegram.
- SmoothTrail est adapté du tweet de 128_mhz.
- SokobanLevel1 semble être le premier niveau du puzzle Sokoban de Hiroyuki Imabayashi. SokobanLevel2 est le niveau 452 du jeu Ionic Catalysts XI.
Les scènes Voxel ont été rendues dans MagicaVoxel par ephtracy. Des remerciements particuliers à Brian Bucklew pour m'avoir démontré la puissance des champs de Dijkstra dans la génération de niveaux de roguelike et à Kevin Chapelier pour un certain nombre de bonnes suggestions. La police utilisée dans l'interface graphique est Tamzen...
Comment construire
L'interpréteur MarkovJunior est une application console qui ne dépend que de la bibliothèque standard. Téléchargez .NET Core (la dernière version en cours) pour Windows, Linux ou macOS et exécutez
dotnet run --configuration Release MarkovJunior.csproj
Vous pouvez également télécharger et exécuter la dernière version pour Windows.
Ne dispense pas du .Net Core du dessus!!!
Les résultats générés sont placés dans le dossier de sortie. Editez models.xml pour modifier les paramètres du modèle. Ouvrez les fichiers .vox avec MagicaVoxel.
L'interpréteur MarkovJunior est une application console qui ne dépend que de la bibliothèque standard. Téléchargez .NET Core (la dernière version en cours) pour Windows, Linux ou macOS et exécutez
dotnet run --configuration Release MarkovJunior.csproj
Vous pouvez également télécharger et exécuter la dernière version pour Windows.
Ne dispense pas du .Net Core du dessus!!!
Les résultats générés sont placés dans le dossier de sortie. Editez models.xml pour modifier les paramètres du modèle. Ouvrez les fichiers .vox avec MagicaVoxel.
Petits tests :)
Il faut mettre tous les fichiers du dossier models en "Tempo" et ne garder que le fichier xml concerné pour éviter tous les autres calculs!
Les résultats seront dans le dossier Output (images .PNG et .Vox )
Les résultats seront dans le dossier Output (images .PNG et .Vox )
|
CarmaTower
Jusqu'à plus ample informé il semble que l'on puisse modifier, pour un résultat probant, que la hauteur (maxi 64) dans le dossier models de la racine (ligne 4 et 5) ce qui permet d'avoir des tours de cette hauteur dans MagicaVoxel! Hauteur de la matrice Magica plafonnée à 240. |
Pour la maison moderne, même pas besoin de modifier le programme donne de lui-même 3 variations :)
On les recharge dans MagicaVoxel!En faire des "Patterns" pour pouvoir les prendre à discrétion!
On va bien sûr pouvoir rendre les fenêtres transparentes, donner quelques matériaux aux différentes couleurs
Pivoter, agrandir, modifier, multiplier... que sais-je !
Encore un infini des possibles au coin de la rue!
On les recharge dans MagicaVoxel!En faire des "Patterns" pour pouvoir les prendre à discrétion!
On va bien sûr pouvoir rendre les fenêtres transparentes, donner quelques matériaux aux différentes couleurs
Pivoter, agrandir, modifier, multiplier... que sais-je !
Encore un infini des possibles au coin de la rue!