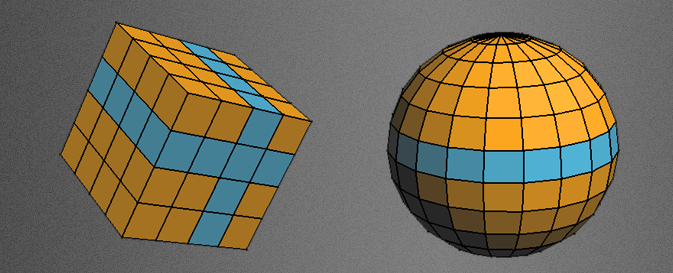Le Modélisateur Débutant - Page 2
Pas de Nurbs ici!
Il y a de nombreux types différents de modélisation 3D avec un ordinateur ces jours-ci, depuis le dessin technique de CAO qui transforme des esquisses plates en bâtiments jusqu'à des applications virtuelles de tours de potier. Cet aperçu concerne la modélisation de polygones à l'aide de surfaces de Sub-division. Il n'inclut aucune information sur une autre forme de modélisation connue sous le nom de NURBS.
Les NURBS, abréviation de Non-Uniform Rational B-spline, est une technique d'infographie pour dessiner des courbes. Une courbe NURBS est définie par un ensemble de points de contrôle pondérés, l'ordre de la courbe et un vecteur nœud. Les NURBS sont des généralisations à la fois des B-Splines et des courbes de Bezier, la principale différence étant la pondération des points de contrôle qui les rend rationnelles (les B-splines non rationnelles sont un cas particulier de B-splines rationnelles; en pratique la plupart des courbes Nurbs sont Non rationnelles).
Et devinez quoi? Nous n'en discuterons pas du tout ici!
Pourquoi?
La subdivision a gagné la popularité courante longtemps après que la modélisation des NURBS était bien établie. Il est généralement excepté que la modélisation en Sub-D est plus libre et plus fluide qu'avec les Splines. Les grands studios de cinéma ont adopté les surfaces de subdivision avec Pixar, étant l'un des premiers à développer et à les adopter complètement.
Les NURBS, abréviation de Non-Uniform Rational B-spline, est une technique d'infographie pour dessiner des courbes. Une courbe NURBS est définie par un ensemble de points de contrôle pondérés, l'ordre de la courbe et un vecteur nœud. Les NURBS sont des généralisations à la fois des B-Splines et des courbes de Bezier, la principale différence étant la pondération des points de contrôle qui les rend rationnelles (les B-splines non rationnelles sont un cas particulier de B-splines rationnelles; en pratique la plupart des courbes Nurbs sont Non rationnelles).
Et devinez quoi? Nous n'en discuterons pas du tout ici!
Pourquoi?
La subdivision a gagné la popularité courante longtemps après que la modélisation des NURBS était bien établie. Il est généralement excepté que la modélisation en Sub-D est plus libre et plus fluide qu'avec les Splines. Les grands studios de cinéma ont adopté les surfaces de subdivision avec Pixar, étant l'un des premiers à développer et à les adopter complètement.
Qu'est-ce que la Modélisation de SubDivision?
La modélisation de la subdivision permet au modélisateur de créer un modèle lissé (subdivisé) à partir d'un modèle de résolution inférieure (connu sous le nom de cage de contrôle ou de cage).
Dans l'exemple ci-dessous, vous pouvez voir un cube de polygone de base qui servira de cage de contrôle. Certains programmes vous permettent de subdiviser par étapes et d'autres programmes seront définis à un très haut niveau de sous-division par défaut. Dans cet exemple, vous pouvez toujours voir le cube en forme de contour vous montrant que cet objet, même quand il ressemble à une Sphère qui est toujours un objet à six faces.
Dans l'exemple ci-dessous, vous pouvez voir un cube de polygone de base qui servira de cage de contrôle. Certains programmes vous permettent de subdiviser par étapes et d'autres programmes seront définis à un très haut niveau de sous-division par défaut. Dans cet exemple, vous pouvez toujours voir le cube en forme de contour vous montrant que cet objet, même quand il ressemble à une Sphère qui est toujours un objet à six faces.
|
`Les surfaces de subdivision sont utilisées pour créer des surfaces lisses à partir de maillages arbitraires. Les surfaces de subdivision sont définies comme la limite d'un processus de raffinement infini. Elles ont été introduites simultanément par Edwin Catmull et Jim Clark et par Daniel Doo et Malcom Sabin en 1978. Peu de progrès ont été réalisés jusqu'en 1995, lorsque Ulrich Reif a résolu le comportement des surfaces de subdivision près des sommets extraordinaires. C'est ce que disent tous les livres. Mais qu'est-ce que cela signifie pour moi, un nouveau venu dans ce monde déroutant de la modélisation Polygonale?
|
Il est parfois nécessaire de modéliser avec de la géométrie déjà subdivisée. Cela vous permet de voir votre maillage dans son état final, lissé comme vous allez le long. Un inconvénient est que vous ne pouvez pas vous concentrer sur la disposition et la position des polygones dans la géométrie sous-jacente (ou Cage). Si vous ne n'utilisez pas et ne sortez pas du mode Subdivision, vous risquez de vous retrouver avec un maillage désordonné.
Maillage Désordonné
Par Maillage désordonné, je me réfère à un modèle polygonal qui semble très bien quand il est Sub-divisé, mais semble un désordre complet quand il ne l'est pas. Il peut avoir des sommets / points, des arêtes ou des faces polygonales qui se croisent sur beaucoup d'endroits. Cela semble désordonné, mais surtout il peut créer des problèmes à des étapes ultérieures du projet.
Par exemple:
Si des coordonnées UV sont créées sur le maillage de base, il peut être nécessaire de les modifier en vue UV pour éviter l'étirement (dans la plupart des programmes, les faces polygonales doivent être aplaties dans les vues UV et ne pas avoir de points croisés).
Lors de la manipulation d'un personnage avec un système d'articulations la manière habituelle est d'avoir les groupes d'effet des points d'articulations avec des degrés différents d'influence (habituellement appelé pondération). Par conséquent, il s'ensuit que si les points sont tous en désordre et se croisement les uns sur les autres, il rendra le travail entier beaucoup plus difficile. Évidemment, cela est différent d'un logiciel à l'autre.
Par exemple:
Si des coordonnées UV sont créées sur le maillage de base, il peut être nécessaire de les modifier en vue UV pour éviter l'étirement (dans la plupart des programmes, les faces polygonales doivent être aplaties dans les vues UV et ne pas avoir de points croisés).
Lors de la manipulation d'un personnage avec un système d'articulations la manière habituelle est d'avoir les groupes d'effet des points d'articulations avec des degrés différents d'influence (habituellement appelé pondération). Par conséquent, il s'ensuit que si les points sont tous en désordre et se croisement les uns sur les autres, il rendra le travail entier beaucoup plus difficile. Évidemment, cela est différent d'un logiciel à l'autre.
Catmull-Clark ou Doo-Sabin?
Les routines d'algorithme de Sub-division (les mathématiques faisant la sous-division derrière les scènes) peuvent venir dans des saveurs différentes et semblent être nommées d'après les gars intelligents qui les ont créés. Un très commun est Catmull Clark et peut être trouvé dans la plupart des grands package 3D disponibles aujourd'hui et pour être honnête, vous n'avez pas vraiment besoin de savoir qu'il est utilisé à moins que vous prévoyez d'aider à travailler sur le développement du logiciel. Même ZBrush utilise ce type de sous-division dans ses fonctionnalités Sub-D multi-résolution.
|
Source Wikipedia; le Dr. Edwin Catmull (né en 1945 en Virginie-Occidentale) est un informaticien qui a contribué à de nombreux développements importants en infographie. Au début de sa vie, Catmull a trouvé son inspiration dans les films de Disney tels que Peter Pan et Pinocchio et rêvait de devenir un animateur de long métrage. Cependant, il a évalué ses chances de façon réaliste et a décidé que ses talents se trouvaient ailleurs.
Au lieu de poursuivre une carrière dans l'industrie cinématographique, il s'est inscrit aux programmes de physique et d'informatique de l'Université de l'Utah. C'est là qu'il a réalisé trois découvertes graphiques fondamentales: le Z-buffer, le mappage de texture et les patches bicubiques. À l'université, il a inventé des algorithmes pour l'anti-aliasing et le rendu des surfaces de subdivision et a créé, en 1974, sa première contribution à l'industrie cinématographique, une version animée de sa main gauche pour Futureworld, la suite de science-fiction du film Westworld et le Premier film à utiliser l'infographie 3D. Après avoir quitté l'université, Catmull a fondé le Computer Graphics Lab au New York Institute of Technology. En 1979 il est allé travailler pour George Lucas à Lucasfilm. C'est à Lucasfilm qu'il a aidé à développer la technologie de composition numérique d'images utilisée pour combiner plusieurs images d'une manière convaincante. Plus tard, en 1986, Catmull a fondé Pixar avec Alvy Ray Smith. Chez Pixar, Catmull a été un développeur clé du système de rendu RenderMan utilisé dans des films tels que Toy Story et Finding Nemo. En 1993, l'Académie des arts et des sciences du cinéma a présenté à Catmull son premier Oscar pour "le développement du logiciel Renderman qui produit des images utilisées dans les images animées à partir de descriptions informatiques en 3D de la forme et de l'apparence". Un Award "pour les inventions pionnières dans le Digital Image Compositing". Enfin, en 2001, il a reçu un Oscar "pour les progrès significatifs dans le domaine du rendu de films illustré par RenderMan Pixar." |
L'Egde Loop (la boucle d'arêtes)
Les boucles de bordure et la connaissance de leur utilisation sont essentielles pour apprendre à modéliser les surfaces de subdivision
Essentiellement, une boucle d'arêtes est une ligne d'arêtes de polygones qui suivent un chemin continu autour d'un objet. Lorsque l'arête atteint tout le contour du modèle et revient sur lui-même, il forme une boucle d'arête.
Essentiellement, une boucle d'arêtes est une ligne d'arêtes de polygones qui suivent un chemin continu autour d'un objet. Lorsque l'arête atteint tout le contour du modèle et revient sur lui-même, il forme une boucle d'arête.
Elles sont couramment rencontrées dans tous les modèles de subdivision, mais elles sont devenues synonymes de la modélisation des personnages organiques. Par exemple, elles sont souvent assimilées aux muscles qui forment l'anneau autour d'un œil. De bonnes boucles d'arêtes permettent une bonne déformation de l'animation.
La boucle d'arêtes ne doit pas nécessairement être au centre d'un objet. Elle peut former le bord extérieur ou un bord intérieur formant un trou ouvert dans le treillis.
Lorsqu'une boucle d'arêtes rencontre une jonction de quatre arêtes, si elle continue le long du chemin du milieu, elle reste comme une boucle d'arêtes. Lorsqu'elle prend l'une des deux autres branches, cela termine la boucle. Si la boucle périphérique rencontre une jonction de 3 arêtes cela la termine également. terminer
Lorsqu'une boucle d'arêtes rencontre une jonction de quatre arêtes, si elle continue le long du chemin du milieu, elle reste comme une boucle d'arêtes. Lorsqu'elle prend l'une des deux autres branches, cela termine la boucle. Si la boucle périphérique rencontre une jonction de 3 arêtes cela la termine également. terminer
|
Il y a eu beaucoup de discussions sur l'avenir de la modélisation sub-D et donc des boucles d'arêtes. Comme des logiciels innovants tels que Pixologics ZBrush et des packages de modélisation basés sur du Voxel comme 3DCoat permettent au sculpteur numérique de créer des maillages de polygones de plusieurs millions de pixels, la pertinence des boucles d'arêtes s'efface. Bien qu'il y ait encore une cage de polygones faibles dans l'équation et bien sûr l'animation nécessitant une pondération, les boucles périphériques sont importantes.
|
Les Polygones à 4 et 5 côtés et les Pôles
Les modèles polygonaux sont constitués de faces polygonales. Les faces sont constituées d'arêtes et de points. La plupart des packages de modélisation 3D prennent en charge l'utilisation de polygones de plus de 4 côtés (appelés N-Gons).
Un pôle est un point (vertice) qui a plus de 4 arêtes entrant en lui. Chaque fois que vous effectuez une extrusion sur un maillage à base de quads vous devrez créer des pôles, à la fois de 3 et 5 arêtes de pôles. Ceux-ci peuvent être appelés le N-Pôle (5 arêtes se réunissant en un point) et le E-Pôle (3 arêtes se rencontrant en un point)
Un exemple de ce qui précède est montré dans l'image ci-dessous. La tête à droite se compose entièrement de Quads et donne un maillage Subdivisé très prévisible. La tête de la gauche est pleine de N-Gons et de Tri et une fois sous-divisée des pincement et irrégularités dans le maillage peuvent être vus. Les deux modèles contiennent cependant des N-Pôles à cinq arêtes.
Image manquante dans l'article l'original!
Qu'en est-il est-ce alors? Qui a raison et quelles sont les règles? Ces questions abondent dans les forums pour chaque package de Subdivision disponible et voici une sélection de réponses que j'ai pris des livres, des forums, des magazines, du matériel de formation et de la bonne vieille expérience de la mode de ces dernières années:
La modélisation avec tout Quads est bonne pour plusieurs raisons. Tout d'abord, lorsque vous subdivisez un quad, vous obtenez un résultat très prévisible. Deuxièmement, si vous modèlisez avec 100% de quads par défaut, vous avez également modélisé 100% Triangles si nécessaire. Vous frappez simplement le bouton qui divise les quads en deux (habituellement quelque chose comme triple ou tessellate). Ainsi, un maillage avec 2000 Quads peut être rapidement et prévisiblement transformé en 4000 triangles.
Pas tous les modélisateurs ne sont d'accord avec cela et vous trouverez des articles pour soutenir les deux théories. Steve Stahlberg par exemple (VO)
Un pôle est un point (vertice) qui a plus de 4 arêtes entrant en lui. Chaque fois que vous effectuez une extrusion sur un maillage à base de quads vous devrez créer des pôles, à la fois de 3 et 5 arêtes de pôles. Ceux-ci peuvent être appelés le N-Pôle (5 arêtes se réunissant en un point) et le E-Pôle (3 arêtes se rencontrant en un point)
Un exemple de ce qui précède est montré dans l'image ci-dessous. La tête à droite se compose entièrement de Quads et donne un maillage Subdivisé très prévisible. La tête de la gauche est pleine de N-Gons et de Tri et une fois sous-divisée des pincement et irrégularités dans le maillage peuvent être vus. Les deux modèles contiennent cependant des N-Pôles à cinq arêtes.
Image manquante dans l'article l'original!
Qu'en est-il est-ce alors? Qui a raison et quelles sont les règles? Ces questions abondent dans les forums pour chaque package de Subdivision disponible et voici une sélection de réponses que j'ai pris des livres, des forums, des magazines, du matériel de formation et de la bonne vieille expérience de la mode de ces dernières années:
La modélisation avec tout Quads est bonne pour plusieurs raisons. Tout d'abord, lorsque vous subdivisez un quad, vous obtenez un résultat très prévisible. Deuxièmement, si vous modèlisez avec 100% de quads par défaut, vous avez également modélisé 100% Triangles si nécessaire. Vous frappez simplement le bouton qui divise les quads en deux (habituellement quelque chose comme triple ou tessellate). Ainsi, un maillage avec 2000 Quads peut être rapidement et prévisiblement transformé en 4000 triangles.
Pas tous les modélisateurs ne sont d'accord avec cela et vous trouverez des articles pour soutenir les deux théories. Steve Stahlberg par exemple (VO)
Si vous apprenez à modéliser, apprenez à modéliser avec tout Quads. En général la modélisation est une étape dans un processus: Concept Art> Modélisation> UV'ing> Texturing> Rigging / Muscles> Animation. Donc, si vous êtes un modélisateur travaillant dans le cadre d'une équipe, vous aurez une direction très claire sur la façon dont le maillage doit être créé. Si l'instruction est "tout va" alors tout va bien. Si l'exigence est un nombre limité de polygones et tous les Quads, mais vous n'avez jamais pris le temps d'apprendre à modéliser de cette façon, alors vous perdez.
Il est, bien sûr, plus facile de modéliser simplement sans contrainte et se retrouver avec 3, 4, 5 et polygones plus polyvalents. Il peut être libérateur de modèliser juste en jetant la prudence au vent et de penser à la forme et la forme de la façon dont un sculpteur traditionnel peut faire. Certains modélisateurs très qualifiés en effet modèlisent de cette façon et créent des modèles impressionnants.
Les N-Gons (Polygones de plus de 4 côtés) ne fonctionnent pas dans tous les packages de modélisation de subdivision. Donc, si vous voulez une compatibilité multi plate-forme maximale, utilisez uniquement Quads et Triangles. Même les packages qui peuvent subdiviser les N-Gons peuvent donner des résultats imprévisibles quand ils sont subdivisés.
Beaucoup d'experts en modélisation semblent s'en tenir au mantra du "Tout Quads, sauf là où il faut avoir un Tri". Modélisez avec des quads autant que possible et / où vous luttez pour atteindre cet objectif utilisez un triangle, mais essayez de les cacher sur le modèle au cas où ils provoquent un problème au moment de la subdivision. Les problèmes auxquels je fais référence sont généralement des facettes du maillage lissé ou une sorte d'erreur de géométrie.
Un modèle qui semble bon et bien subdivisé à la base ou en pose de repos peut ne pas l'être quand il est animé. Essayez de garder cela à l'esprit lorsque vous construisez votre géométrie.
Qu'en est-il de la modélisation pour les jeux? Le grand défi pour les créateurs de jeux ces dernières années a été de maintenir le nombre de polygones assez bas pour que le jeu ne soit pas affecté. Une façon dont les programmeurs de jeu ont été en mesure de contourner cela est d'utiliser des cartes qui simulent des détails élevés sur la surface des modèles à faible détails. Un type très spécialisé de carte est appelé une carte normale (Normal Map). Ces cartes prennent des informations à partir de modèles de détails élevés qui peuvent ensuite être utilisés sur une version polygone basse résolution pour simuler les détails. Le modèle n'est pas plus complexe mais l'expérience visuelle est grandement améliorée. Les moteurs de jeu convertissent le maillage à tous les triangles aussi utiliser des triangles est lieu commun. Toutefois, faire un quadrillage 100% quad peut aussi vous donner un prédictible 100% Tri si nécessaire.
Il est, bien sûr, plus facile de modéliser simplement sans contrainte et se retrouver avec 3, 4, 5 et polygones plus polyvalents. Il peut être libérateur de modèliser juste en jetant la prudence au vent et de penser à la forme et la forme de la façon dont un sculpteur traditionnel peut faire. Certains modélisateurs très qualifiés en effet modèlisent de cette façon et créent des modèles impressionnants.
Les N-Gons (Polygones de plus de 4 côtés) ne fonctionnent pas dans tous les packages de modélisation de subdivision. Donc, si vous voulez une compatibilité multi plate-forme maximale, utilisez uniquement Quads et Triangles. Même les packages qui peuvent subdiviser les N-Gons peuvent donner des résultats imprévisibles quand ils sont subdivisés.
Beaucoup d'experts en modélisation semblent s'en tenir au mantra du "Tout Quads, sauf là où il faut avoir un Tri". Modélisez avec des quads autant que possible et / où vous luttez pour atteindre cet objectif utilisez un triangle, mais essayez de les cacher sur le modèle au cas où ils provoquent un problème au moment de la subdivision. Les problèmes auxquels je fais référence sont généralement des facettes du maillage lissé ou une sorte d'erreur de géométrie.
Un modèle qui semble bon et bien subdivisé à la base ou en pose de repos peut ne pas l'être quand il est animé. Essayez de garder cela à l'esprit lorsque vous construisez votre géométrie.
Qu'en est-il de la modélisation pour les jeux? Le grand défi pour les créateurs de jeux ces dernières années a été de maintenir le nombre de polygones assez bas pour que le jeu ne soit pas affecté. Une façon dont les programmeurs de jeu ont été en mesure de contourner cela est d'utiliser des cartes qui simulent des détails élevés sur la surface des modèles à faible détails. Un type très spécialisé de carte est appelé une carte normale (Normal Map). Ces cartes prennent des informations à partir de modèles de détails élevés qui peuvent ensuite être utilisés sur une version polygone basse résolution pour simuler les détails. Le modèle n'est pas plus complexe mais l'expérience visuelle est grandement améliorée. Les moteurs de jeu convertissent le maillage à tous les triangles aussi utiliser des triangles est lieu commun. Toutefois, faire un quadrillage 100% quad peut aussi vous donner un prédictible 100% Tri si nécessaire.
De Quel Programme 3D ai-je Besoin?
Donc, à la question que vous aurez déjà posée et peut-être même avez-vous déjà répondu. Quel programme allez-vous utiliser pour sculpter ces polygones dont nous parlons? Il n'y a pas de bonne réponse ici (sauf si vous travaillez pour l'une des sociétés qui vendent le logiciel).
Vous choisirez votre logiciel en fonction d'un certain nombre de questions et de choix:
etc ...
Vous choisirez votre logiciel en fonction d'un certain nombre de questions et de choix:
- Combien puis-je me permettre? Si la réponse est rien alors regardez les solutions libres.
- Est-ce que je veux plus que de la modélisation? Si oui, vous devez examiner les solutions plus complètes qui incluent la texturation, les articulations, l'animation et les solutions de rendu complètes.
- Est-ce que je veux un travail dans un studio qui se spécialise dans un seul programme (3DStudio Max par exemple)
etc ...