Libre traduction du PDF sur l'hélice variable de Bemfarmer
Script Helix à hauteur variable pour Moment of Inspiration
Par Brian McMillin, 1 mai 2014
La commande régulière Helix de MoI crée une hélice à pas constant, ainsi que de rayon variable,
à courbes (conique), et hélice plate. Il est préférable à ce script, pour une hélice à pas non variable.
Une hélice régulière a un angle de pas constant.
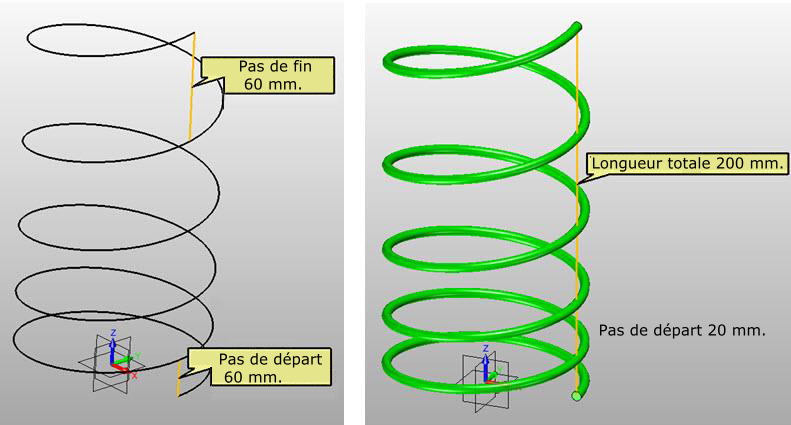
Ce script crée une hélice généralisée qui peut contenir un pas variable, et un rayon variable.
Ce texte est basé sur les mathématiques qui sont bien décrits dans le lien suivant. Le lien
comprend plusieurs graphiques, ainsi que les erreurs d'orthographe, y compris les variations de l'orthographe de thêta. http:www.zwsoft.com/forum/thread-2980-1-1.html
Par Brian McMillin, 1 mai 2014
La commande régulière Helix de MoI crée une hélice à pas constant, ainsi que de rayon variable,
à courbes (conique), et hélice plate. Il est préférable à ce script, pour une hélice à pas non variable.
Une hélice régulière a un angle de pas constant.
Ce script crée une hélice généralisée qui peut contenir un pas variable, et un rayon variable.
Ce texte est basé sur les mathématiques qui sont bien décrits dans le lien suivant. Le lien
comprend plusieurs graphiques, ainsi que les erreurs d'orthographe, y compris les variations de l'orthographe de thêta. http:www.zwsoft.com/forum/thread-2980-1-1.html
Pour ré-capituler les mathématiques, il y a trois équations à trois inconnues. Les inconnues à résoudre pour le nombre de tours sont, p1 et p2.
L est la longueur de l'hélice, qui provient du choix des points par l'utilisateur pour les points de début et de fin. Sp est la hauteur de départ de la première courbe de 360 degrés. L'utilisateur entre cette distance.
Ep est la hauteur de fin de la dernière courbe de 360 degrés. L'utilisateur entre cette distance.
N = numTurns = le nombre total de spires de l'hélice. sP et EP déterminent N.
N est résolu par l'aide de la hauteur moyenne (moyenne).
Equation1: N = 2 * L / (sP + EP)
Equation1b: L / N = (sP + EP) / 2
p1 est le paramètre inconnu relatif au pas fixé.
p2 est le paramètre inconnu relatif au pas fixé.
sP , EP, p1 , p2 et ne doivent pas être confondus avec les emplacements qui pourraient être calculés à partir de la tangente à des angles des premier et dernier points de l'hélice.
t est un paramètre qui varie entre 0 et 1, inclus, sur la longueur de l'hélice.
Thêta est l' angle de rotation.
A la fin de la première courbe de degré 360 , theta = 360 = 2PI , et :
numTurns * t = 1 , de sorte que t = 1 / N , de sorte que
Équation2 : sP = p1 + p2 / N
Equation2b : p1 = sP - p2 / N
A la fin de l'hélice , la longueur est donnée par Equation3 :
Equation3 : L = N * p1 + N * p2
Equation3b : L / N = p1 + p2
Equation3c : p1 = L / N - p2
Pour résoudre pour P1 et P2, on met Equation1b égale à Equation3b, puisque chaque équivaut L / N :
P1 + P2 = ( sP + EP) / 2
alors substituer Equation2b pour p1 :
2 * ( SP- p2 / N ) + 2 * P2 = sP + eP
réorganiser et simplifier les termes :
SP - 2 * p2 / N + 2 * p2 = eP
p2 ( ( N-1) / N) = (EP - Sp) / 2
Enfin , cela donne :
Equation4 : p2 = ( N / ( N-1) ) * (EP - Sp) / 2
d'où Equation3c : p1 = L / N - p2
Ainsi, les équations paramétriques finales sont :
x (t ) = ( R1 + R2 * t) * sin ( 360 * Num_turns * t)
y (t ) = ( R1 + R2 * t) * cos ( 360 * Num_turns * t)
z (t ) = N * ( p1 * t + p2 * t * t )
Une valeur non nulle de rayon R2 donne une hélice de rayon variable.
Pour inverser le sens de l'hélice , le sin et cos sont échangés.
Notez que la division par zéro doit être évitée.
Le pas de vis est égale à la tête d'une seule vis de départ. Tête = hauteur * # départ.
L'Angle d'inclinaison est l'angle entre le filetage incliné et un plan perpendiculaire à l'axe du filetage.
L'angle de tangage = angle d'hélice = l'angle de la tangente, par rapport à l'axe central de l'hélice.
L'angle de départ est le complément de l'angle d'attaque. Angle d'attaque = (PI / 2 - angle de tangage).
La hauteur en un point sur une hélice, en utilisant l'angle de la tangente, est la suivante:
Pas = PI * Diamètre * tangente (PI / 2 - angle de tangage).
Pas = PI * Diamètre * tangente (angle d'attaque).
Cela peut être utile pour faire correspondre d'autres courbes.
http://www.eng-tips.com/viewthread.cfm?qid=44686
Un autre lien connexe:
http:forums.autodesk.com/t5/Inventor-General/Variable-Pitch-Helix-by-Equation-Curve/td-p/3507770
Un lien (essentiellement sans relation) qui explique comment enrouler une bande de papier pour faire un tube.
L est la longueur de l'hélice, qui provient du choix des points par l'utilisateur pour les points de début et de fin. Sp est la hauteur de départ de la première courbe de 360 degrés. L'utilisateur entre cette distance.
Ep est la hauteur de fin de la dernière courbe de 360 degrés. L'utilisateur entre cette distance.
N = numTurns = le nombre total de spires de l'hélice. sP et EP déterminent N.
N est résolu par l'aide de la hauteur moyenne (moyenne).
Equation1: N = 2 * L / (sP + EP)
Equation1b: L / N = (sP + EP) / 2
p1 est le paramètre inconnu relatif au pas fixé.
p2 est le paramètre inconnu relatif au pas fixé.
sP , EP, p1 , p2 et ne doivent pas être confondus avec les emplacements qui pourraient être calculés à partir de la tangente à des angles des premier et dernier points de l'hélice.
t est un paramètre qui varie entre 0 et 1, inclus, sur la longueur de l'hélice.
Thêta est l' angle de rotation.
A la fin de la première courbe de degré 360 , theta = 360 = 2PI , et :
numTurns * t = 1 , de sorte que t = 1 / N , de sorte que
Équation2 : sP = p1 + p2 / N
Equation2b : p1 = sP - p2 / N
A la fin de l'hélice , la longueur est donnée par Equation3 :
Equation3 : L = N * p1 + N * p2
Equation3b : L / N = p1 + p2
Equation3c : p1 = L / N - p2
Pour résoudre pour P1 et P2, on met Equation1b égale à Equation3b, puisque chaque équivaut L / N :
P1 + P2 = ( sP + EP) / 2
alors substituer Equation2b pour p1 :
2 * ( SP- p2 / N ) + 2 * P2 = sP + eP
réorganiser et simplifier les termes :
SP - 2 * p2 / N + 2 * p2 = eP
p2 ( ( N-1) / N) = (EP - Sp) / 2
Enfin , cela donne :
Equation4 : p2 = ( N / ( N-1) ) * (EP - Sp) / 2
d'où Equation3c : p1 = L / N - p2
Ainsi, les équations paramétriques finales sont :
x (t ) = ( R1 + R2 * t) * sin ( 360 * Num_turns * t)
y (t ) = ( R1 + R2 * t) * cos ( 360 * Num_turns * t)
z (t ) = N * ( p1 * t + p2 * t * t )
Une valeur non nulle de rayon R2 donne une hélice de rayon variable.
Pour inverser le sens de l'hélice , le sin et cos sont échangés.
Notez que la division par zéro doit être évitée.
Le pas de vis est égale à la tête d'une seule vis de départ. Tête = hauteur * # départ.
L'Angle d'inclinaison est l'angle entre le filetage incliné et un plan perpendiculaire à l'axe du filetage.
L'angle de tangage = angle d'hélice = l'angle de la tangente, par rapport à l'axe central de l'hélice.
L'angle de départ est le complément de l'angle d'attaque. Angle d'attaque = (PI / 2 - angle de tangage).
La hauteur en un point sur une hélice, en utilisant l'angle de la tangente, est la suivante:
Pas = PI * Diamètre * tangente (PI / 2 - angle de tangage).
Pas = PI * Diamètre * tangente (angle d'attaque).
Cela peut être utile pour faire correspondre d'autres courbes.
http://www.eng-tips.com/viewthread.cfm?qid=44686
Un autre lien connexe:
http:forums.autodesk.com/t5/Inventor-General/Variable-Pitch-Helix-by-Equation-Curve/td-p/3507770
Un lien (essentiellement sans relation) qui explique comment enrouler une bande de papier pour faire un tube.